Python is the most popular language among data scientists for its simplicity and flexibility. Additionally, Python includes multiple libraries to deal with Exploratory Data Analysis (EDA). In this post, we'll perform exploratory data analysis on a dataset using Python code to solve each step of the exploration process.

In this example we are using a dataset that contains information about the marketing campaigns of a bank, and the conversions of the customers associated to the campaigns. The original dataset was uploaded in the UCI Machine Learning Repository.

By exploring and asking the right questionsasking the right questions to the data, EDA becomes a powerfulpowerful tool for data scientists, enabling them to perform analysis effectively using data visualizationdata visualization, without complex modeling.

EDA in python involves multiple steps including:

1. Import the libraries

In order to work with data tables, generate exploratory data analysis report, perform mathematical operations, and create a visualization, we need to import a few libraries, which you can do by executing this code:

2. Import the data

To import the data, if we have a CSV containing the dataset, in pandas it is as easy as to use the read_csv method.

It is worth mentioning Lector, an open source library for reading and importing CSV data. Lector is fast and flexible, performing automatic detection of files encoding and customizable type inference, and casting. Currently, Lector is used in Graphext to read CSV datasets optimally.

3. Get to know your data

Determine the number of rows and columns

After importing the data, it's time to get familiar with it. Understanding the size of the data is crucial, as working with thousands of rows is different from working with millions.

(11162, 17)

In this dataset, each row represents a client targeted by a marketing campaign. Therefore, the DataFrame contains 11,162 targeted customers with 17 different variables recorded.

Retrieve the names of the columns

We can get the names of these 17 variables by calling the columns attribute from the DataFrame.

Look up the types of the columns

However, if we use .info(), we will obtain a list of the DataFrame columns together with additional information, such as the data type of each column and the count of non-null values.

Now we know that we have 7 integer columns and 10 columns representing categorical data.

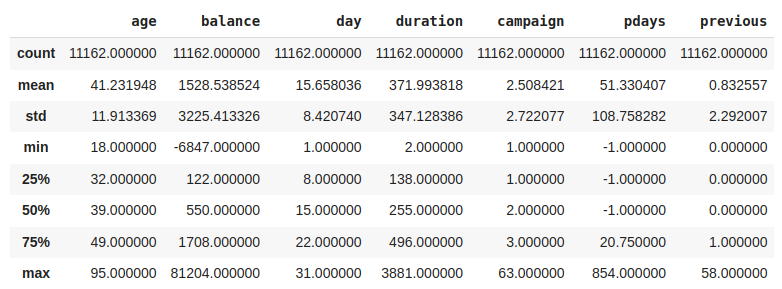
Get the statistics of numerical columns

Another useful method to get to know your data better is .describe() . This method returns the most important metrics for the distributions of the numerical variables, line the percentiles, the mean, the lowest and highest values, etc.

Visualize the first rows of the DataFrame

Another useful method when starting EDA is .head(), which allows you to display the first rows of a DataFrame.

Rename columns

Most variable names are self-explanatory, but some lack of clear names to understand what they contain. Let's rename these variables to improve the analysis. The inplace parameter indicates that the changes will be made directly to the current DataFrame, df.

Get advanced EDA report with pandas-profiling

Use pandas-profiling to generate a report that includes the distributions of all variables, the number of missing values per variable, the summary of all data types and all the relevant correlations found among the variables of the dataset.

4. Prepare your data

Data preparation, also known as data preprocessing, includes all transformations performed on the data before analysis, including data cleaning and feature engineering. This process is done following the next steps:

Deal with Null values

We can start preprocessing our data by looking for null values. When we find null or NaN values there are three approaches to deal with them:

Luckily, this dataset does not have any missing values in its columns. Therefore, there is no need to drop any rows. However, if we had encountered any NaN values, we could have used the dropna function as shown in the code above.

Deal with duplicated samples

Another common issue in data is the presence of duplicated samples. Usually, the data comes from traditional databases, and believe me it is not uncommon to encounter databases where the data is duplicated more than once or twice. Hence, it is important to check if our dataset has any duplicated samples and remove them if necessary using drop_duplicates.

Deal with outliers

Outliers are samples that deviate significantly from the rest of the data, and it is key to handle them to maintain the integrity of our EDA. One typical approach to detect outliers is by calculating the Z-score for each sample, which measures the number of standard deviations std from the mean of the distribution to the . Observations with a Z-score greater than 3 are typically considered outliers.

One way to deal with the outliers is to drop all the rows containing outliers, but depending the variable and the use case we can decide to stick with them.

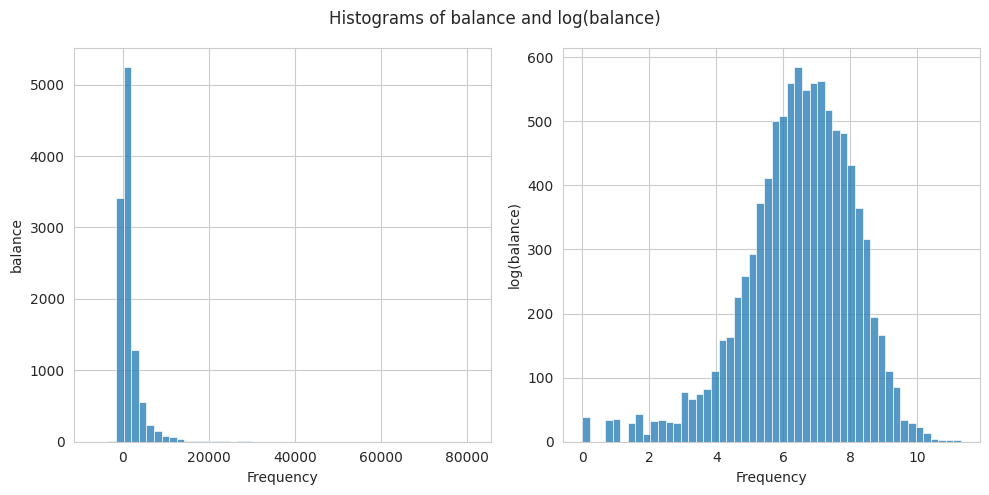
Transform data

The Z-score assumes that the data follows a normal distribution to calculate the number of std away from the mean. Nonetheless, we often find distributions that are not following a normal distribution and are difficult to deal with. To address outliers originating from a right-skewed distribution, such as the balance variable, a possible solution is to apply a log transformation to normalize the distribution first.

5. Analyze your data

Data analysis is key when building a model, and in general when we want to find relationships with respect to a target variable. However, even without a specific target, data analysis can be useful generating relationships among the variables. The main steps to perform the data analysis are:

Distribution of the Target Variable

The dataset we are exploring includes the target variable deposit, which the marketing department aims to optimize. This variable is a boolean indicating whether a customer opened a deposit after being contacted in the marketing campaign. Hence, the objective of the analysis is to identify the strongest relationships between customers who opened a deposit and the other variables.

As Data Scientists the first thing we want to know is the amount of customers that opened a deposit.

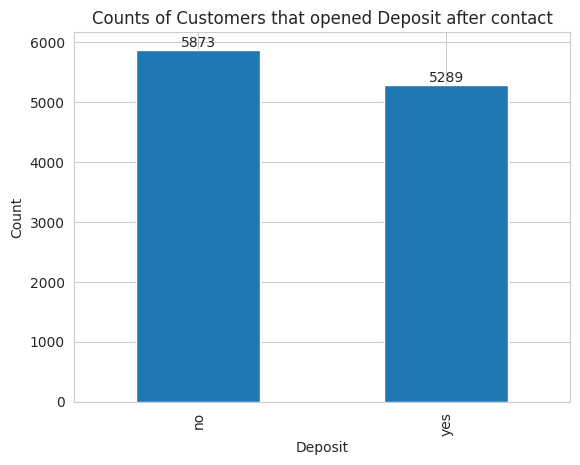
The dataset contains 5289 customers that opened a deposit after being contacted while the remaining 5873 didn’t open the deposit.

Identify relationships with the target variable

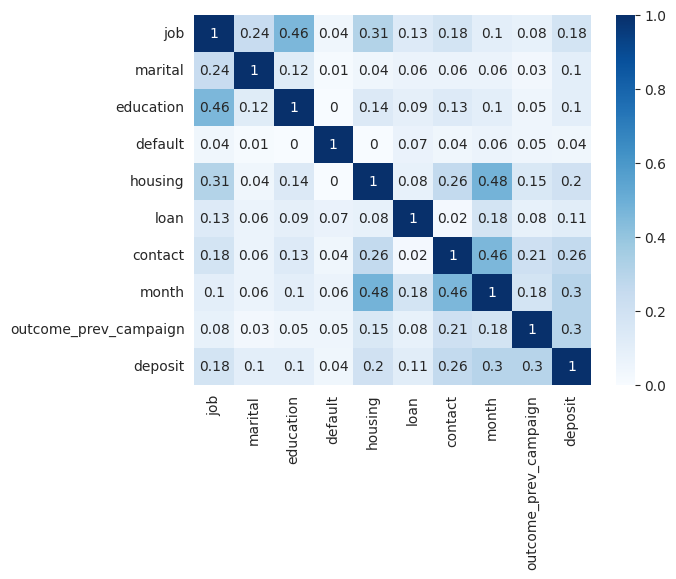
To quickly identify strong relationships with the target variable, we can plot the correlation matrix. However, since we have both categorical and numerical variables, the standard Pearson correlation coefficient, which only detects linear relationships among numerical variables, is not suitable. Instead, we can use Cramer's V coefficient to find relationships among the categorical variables of the dataset.

On the other hand, to learn how the numerical variables are correlated to the binary target we can use the point biserial correlation coefficient.

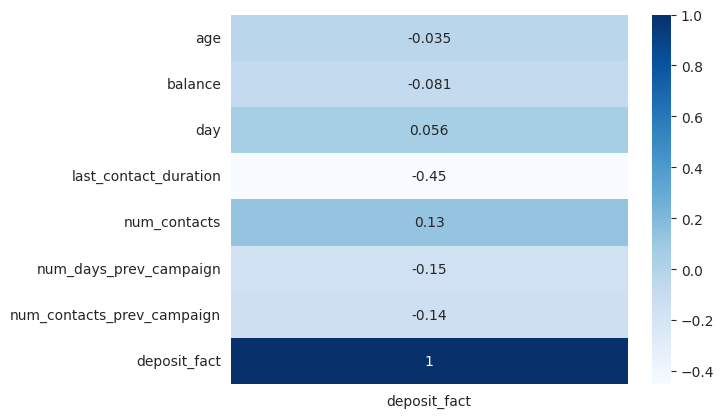
The correlation plots show that the target variable has no strong correlations with other variables but only moderate correlations. There is a correlation between the target variable deposit and last_contact_duration. Additionally, there are moderate correlations between the target and variables such as contact, month, and outcome_prev_campaign.

It is important to note that other methods, such as Mutual Information, are recommended for calculating correlations among all variables regardless of their type.

Visualize relationships with target variable

In the previous sections, we discovered the strongest relationships with the target variable. However, we don't know the nature of these relationships. The best way to understand them is through data visualization. Different types of variables require different types of plots for optimal visualization.