Working with data isn't always ideal. Most of the time, your data will need some processing before it is ready for analysis. Datasets often contain missing, unintelligible or incorrect information and even more annoying ... data that expresses the same concept but is expressed inconsistently.
In the realm of natural language, open questions, tweets or reviews mean data where anyone can write whatever they want. People express the same idea with little variations; capital letters, typos, adding punctuation, accents, acronyms and so on. Not ideal for analysis. We wanted to be able to work around this in Graphext, so we set out to tackle the problem. Simply put, we needed a way to identify words that could be grouped as spelling variations of identical concepts.
'España' and 'Españha' are just spelling variations. We needed a way of picking out words spelt differently but referring to the same concept.
Preprocessing as a Starting Point
We started with an obvious approach; preprocessing words.
It is pretty simple and fast to change words to lowercase as well as removing accents, non-printable characters or extra spaces. Modifying strings like this helped to reduce unnecessary variation between some words but - as we had anticipated - the results were far away from our vision of success and there was too much work left to do.
We preprocessed words to make variations as uniform as possible.
Preprocessing couldn't overcome spelling variations so we turned our attention to defining a way that a computer would be able to understand the similarity between words.
Calculating Similarity with Levenshtein Distance
Levenshtein distance helps to measure the similarity between two words counting the number of characters we have to add, remove or change in one in order to get to another.
Then - the lower this distance is - the greater the similarity between the two words.
Example with Levenshtein Distance of 4
.png)
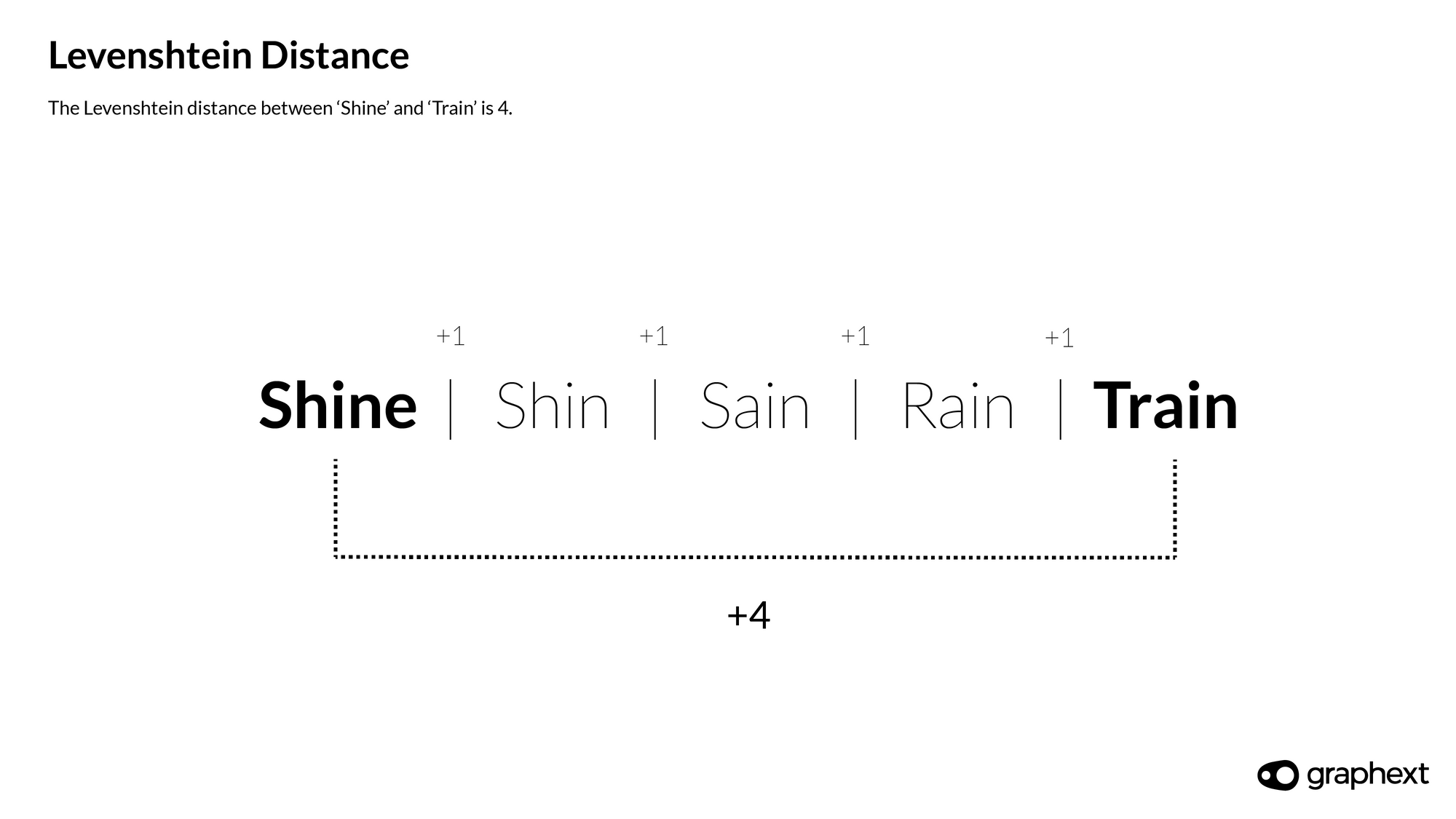
Shine & Train have a Levenshtein distance of 4.
By setting a threshold for similarity, we can use Levenshtein distance to group words with similar spellings.
Example of Grouping with Levenshtein Distance of 1
.png)
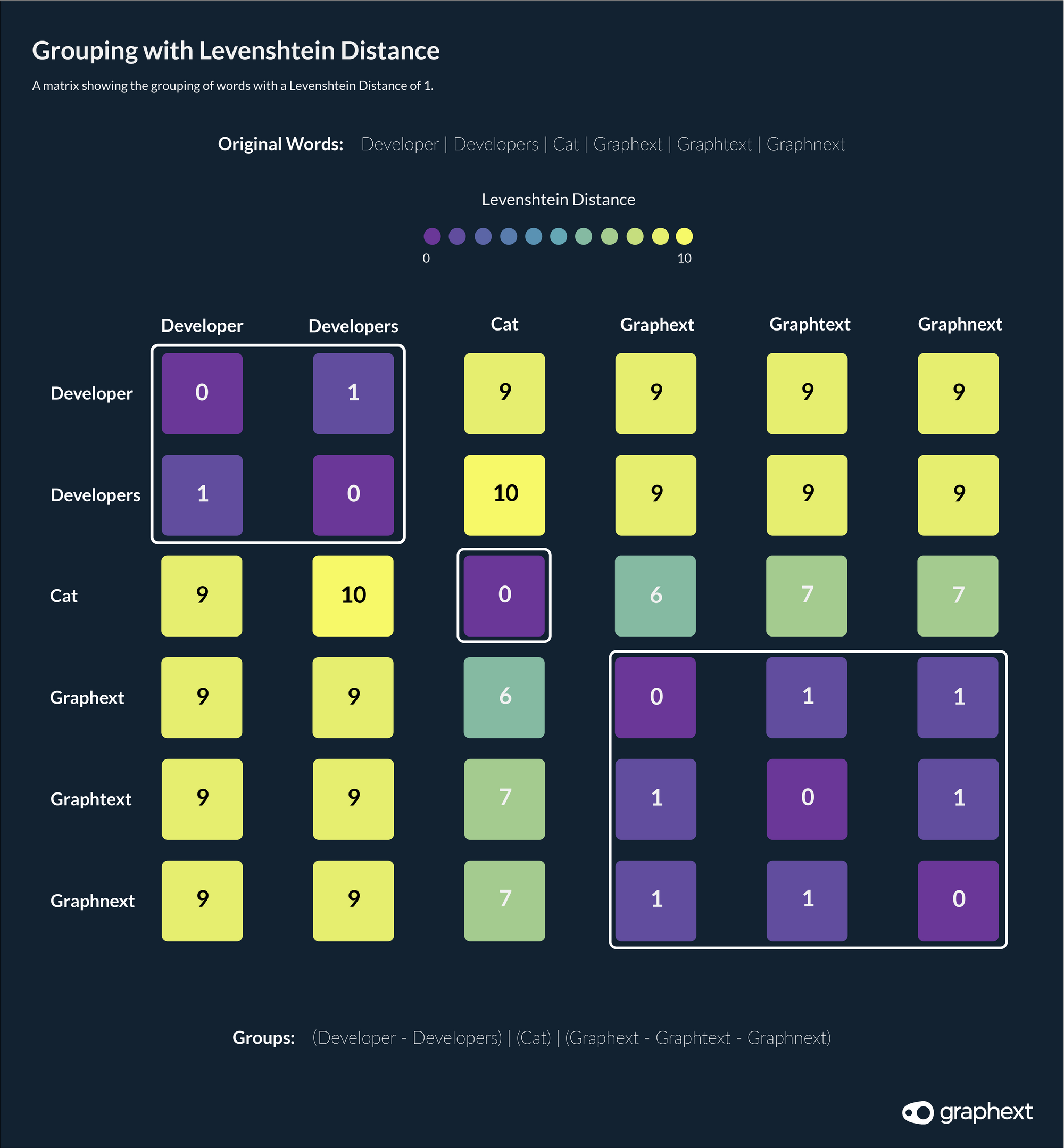
Grouping words with a Levenshtein distance of 1.
Although this solution is, in theory, a good approach - it has some clear drawbacks. Calculating Levenshtein distance is a complex process. Increasing the number of words will, in turn, quadratically increase the number of distances to calculate and resulting in time and memory issues.
Deep Learning Reinforcement
Moving away from the idea of using Levenshtein distance, we realized that we need heavier artillery.
When working with text, it is quite common to use deep learning models that will transform a text into a vector. Usually, those vectors represent the meaning of the words allowing computers to recognise words with similar meanings. However, there are also technologies to transform words into vectors that represent a word's spelling.
To represent spellings in a way that a computer can understand, we used Chars2Vec, a python library offering models that calculate character-based vectors using recurrent neural networks.
One of these is Chars2Vec, a python library offering models that calculate character-based vectors using recurrent neural networks. Choosing a model from Chars2Vec also involved a trade-off between models that created long - and more accurate - vectors but resulted in time and memory issues and models that create short embeddings - poorly representing spellings - but demanding less time and memory. We opted for something in the middle.
The Problem with Clustering
After creating vectors that represented the spelling of words, it became a case of joining similar ones, an easy task for clustering algorithms. But most clustering algorithms define clusters by minimizing the average distance between all considered elements. Because averages are used, words with dissimilar spellings can be clustered together if the overall average is low enough. Imagine we have the following words:
cats - rats- raps- rips- rip
This represents a chain of words where each word is very similar to its predecessor. As a result of the detectable chain, many clustering algorithms would group these words together despite the obvious difference in spelling between cats and rip. We needed a solution that was able to analyze the distance between any two words.
Hierarchical Clustering
With that purpose, we chose Agglomerative Clustering - a hierarchical clustering algorithm that starts out with one cluster for each word and will continuously join two clusters until it meets stopping criteria.
The advantage of this agglomerative clustering is that it allows us to add a distance limit to avoid the problem of word chains - meaning that cats and rip would not be joined. The limit refers to the maximum permissible distance between a pair of words. Setting this limit higher will permit looser joins with bigger distances and correspondingly, lowering its value will result in stricter joins with smaller distances.
With agglomerative clustering, we could start to control the permissible distance between words when considering whether to join them or not.
.png)
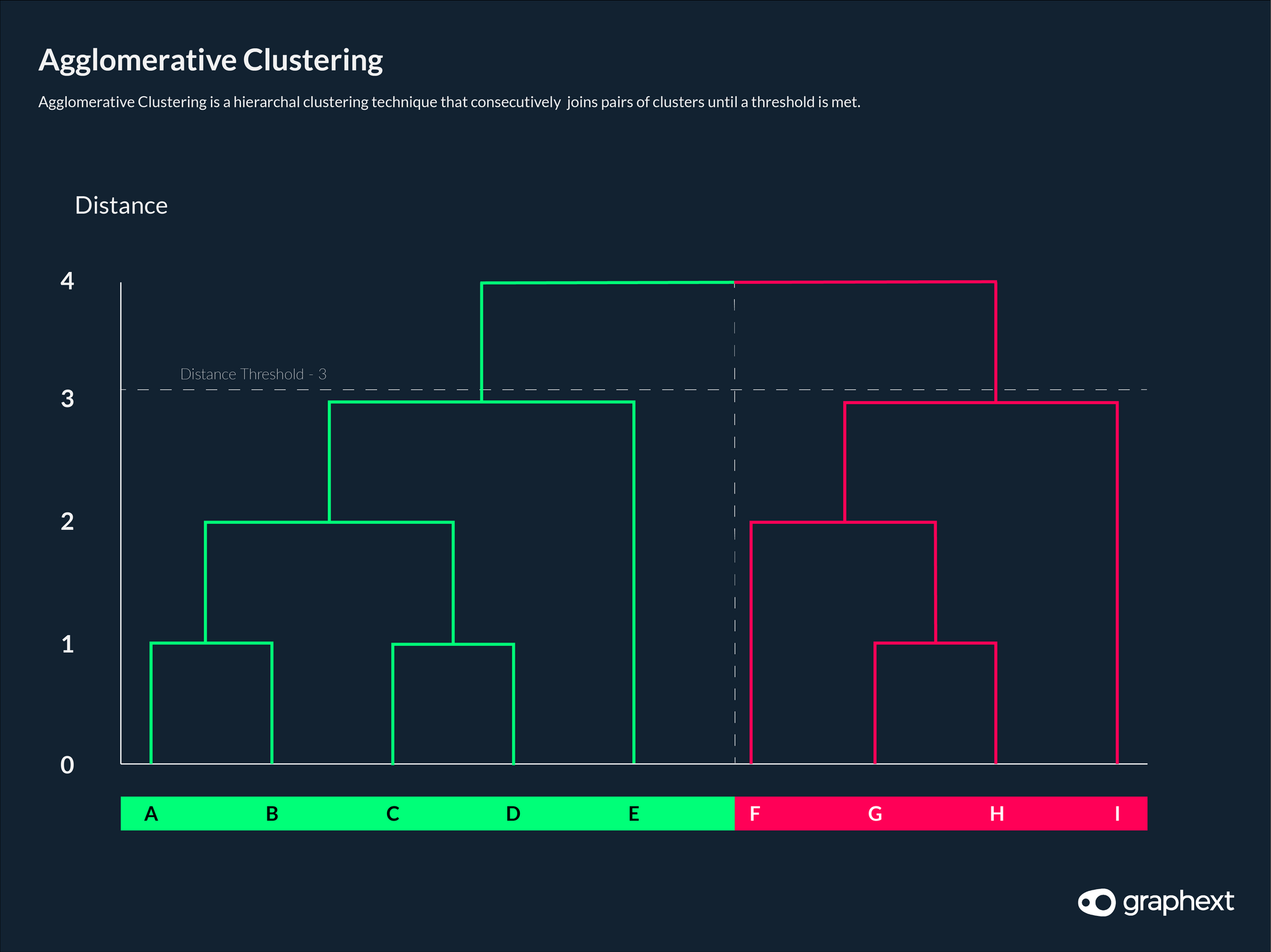
Agglomerative clustering consecutively joins pairs of words until a threshold is met.
Now, we needed to define a suitable limit for maximum distance. Having discarded Levenshtein distance, we are now referring to the distance between two vectors when we talk about distance. Specifically, we are using Euclidean distance - an easy to calculate method yielding good results.
A Side Note on Euclidean Distance
Euclidean distance is a mathematical method that offers computers a fast way to define the distance between two vectors. It can be calculated using the Pythagorean theorem.
.png)
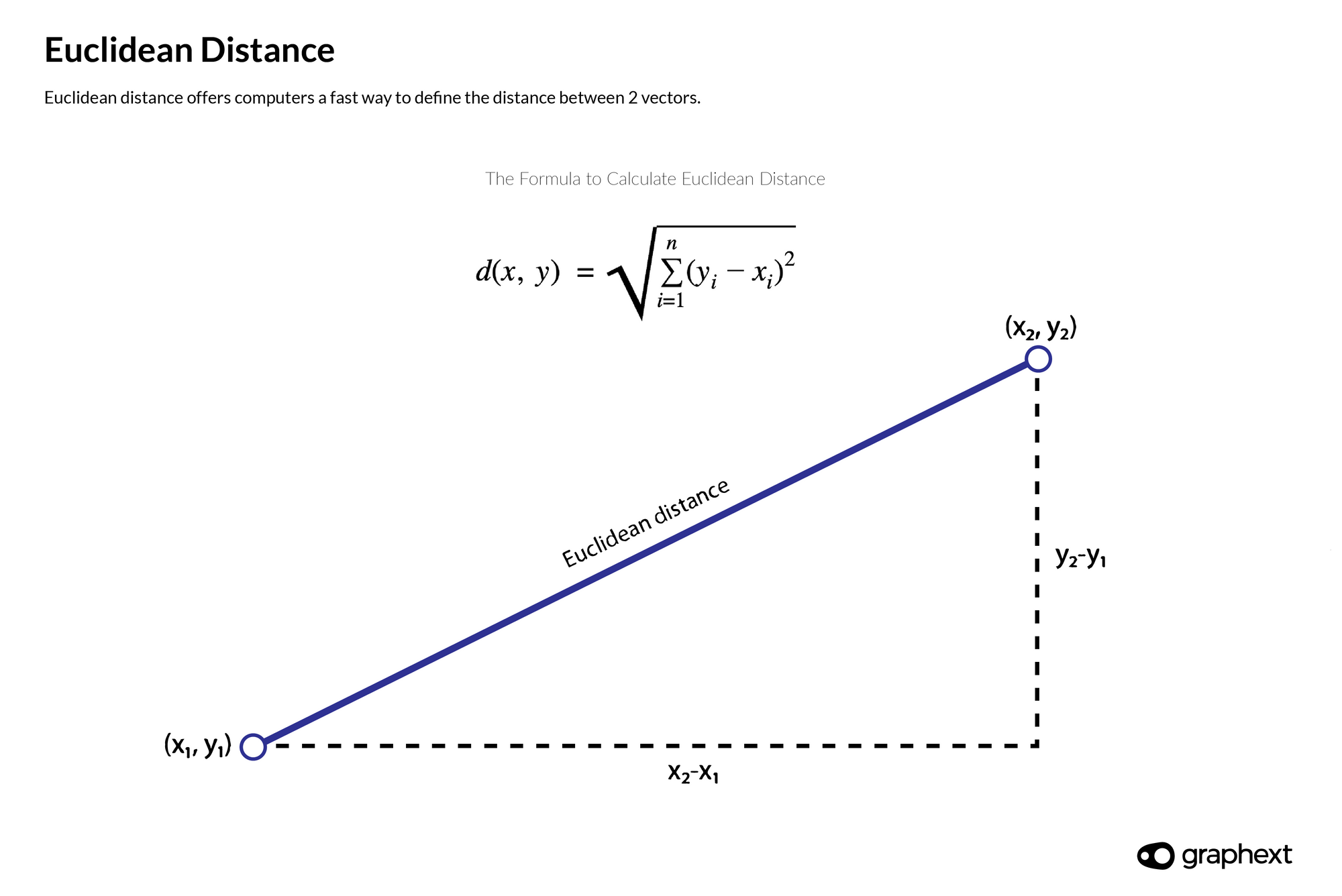
Euclidean distance offers computers a fast way to define the distance between 2 vectors.
But setting a maximum distance threshold is not well suited to measurements using Euclidean distance. The distance between two vectors is a number bigger than zero and non-bounded meaning that the distance measurement is relative to the dataset being used. The solution? A process of increasing and decreasing the distance threshold until it fits your data.
The Final Process
Despite its drawbacks, this process is able to group words with similar spellings together in a way that matches up with our initial vision. Simply put, here's how it works ...
- Preprocessing | Remove unnecessary character variations between words.
- Vectorize | Use Chars2Vec to reduce words to a vector representative of their spelling.
- Agglomerative Clustering | Join vectors based on whether the distance between them falls under a customizable maximum distance threshold.
- Labelling | Labelling the new category of joined words according to the most frequently occurring word.
Using it in Graphext
To open up our solution as part of any type of analysis in Graphext, we created a new enrichment option. During your project setup, open the Data Enrichment tab and choose Group Similar Spellings to start working with it.
Then, tell Graphext which column contains the words you want to join, set a maximum distance threshold and continue to execute your project.
Alternatively, you can open the code editor, find or add the merge_similar_spellings step and change its parameters as you need. For more information on doing this, check out the documentation behind merge_similar_spellings.
Once your project is ready - find the variable with the suffix "-Joined" following your original column name. This new variable contains the result of your word groupings.
