A picture of a population is what most surveys hope to achieve. Who doesn't want to know which essential Tinder personality traits help a person to be successful in love? We're taking a look at the fundamentals of survey theory - sampling & weighting - through the lens of a Pew Research survey that examines American attitudes towards relationships and dating apps in 2021.
"Surveys show that surveys never lie", Natalie Angier, science reporter for the New York Times once said in irony. Badly designed surveys, unrepresentative population samples or poorly designed weights can all introduce bias and spoil survey estimates.
.jpeg)
From political polls to job market reports, surveys have a long history of helping us understand how people think or feel about an issue. But building them can be a tricky process. Bias can easily be introduced if populations aren't sampled fairly or the demographics of respondents aren't weighted in a way that presents a full picture of the community the survey claims to represent.
The Backbone of Survey Theory
The science behind surveys is underpinned by sampling and weighting. Sampling involves selecting a segment of a population to act representatively for the whole population. Weighting is a correction method used to statistically adjust the survey data to improve the accuracy of its estimates.
Survey Sampling
In every survey, a definition of the target population has to be defined. This definition affects which sampling technique is most appropriate. For instance, probability sampling is used in cases where the target is the whole population, whereas non-probability sampling is used in cases where the target is a subgroup with very specific characteristics.
Probability Sampling
Using probability sampling methods means that everyone in the target population has a chance of being chosen. Probability sampling is more expensive and time-consuming but usually leads to better results.
.png)
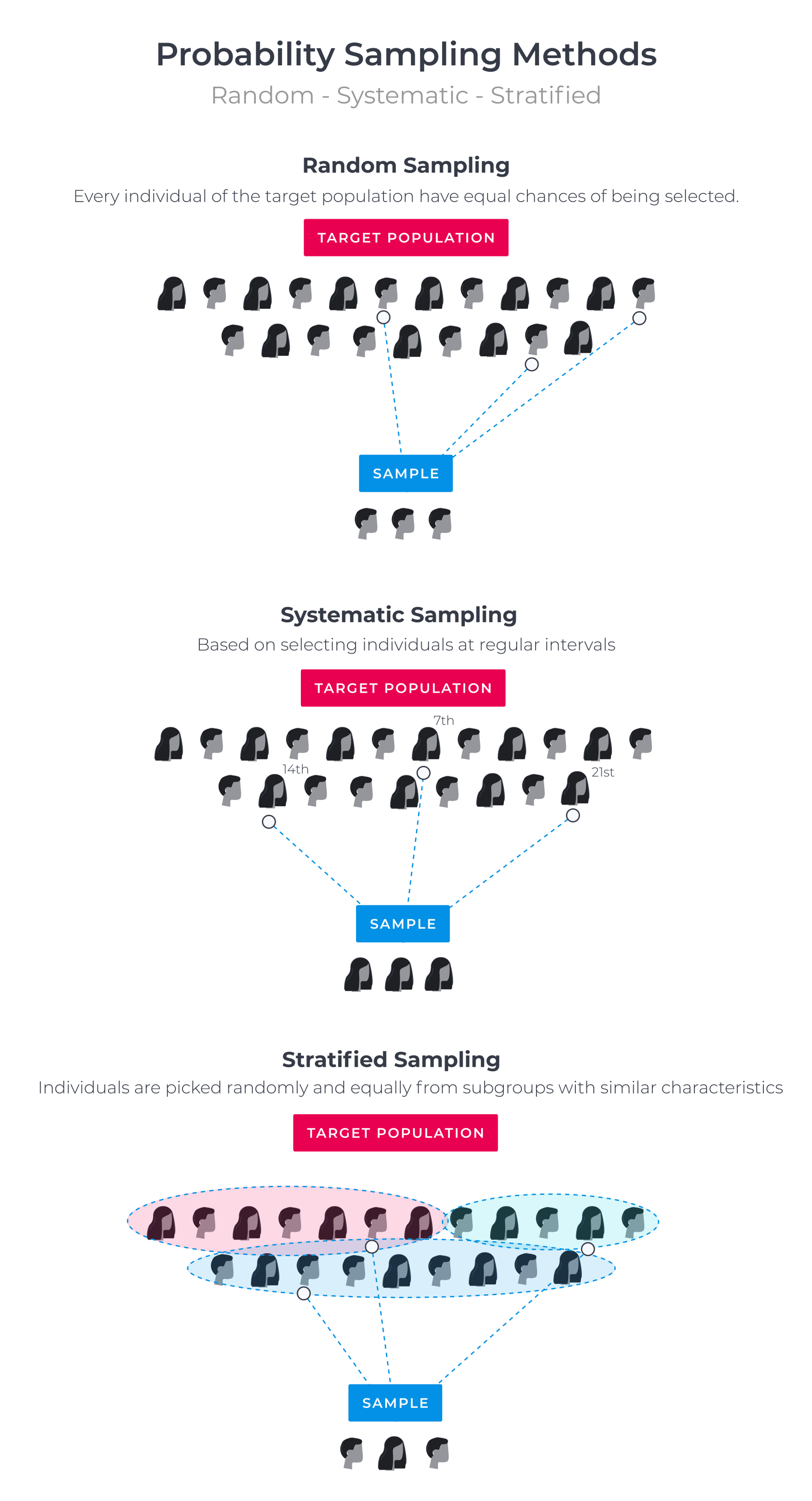
Common Probability Sampling Methods
- Simple random sampling - Every individual of the target population have equal chances of being selected.
- Systematic sampling - Based on selecting individuals at regular intervals. For instance, to derive a sample size of 100 from a target population of 1000, every 10th individual would be selected.
- Stratified sampling - Individuals are picked randomly and equally from subgroups with similar characteristics. Best used when we know that specific variable distributions vary from one group to another.
Non-Probability Sampling
Non-probability sampling methods are used when we don't have a full sample of the population. As a result, some individuals have no chance of being selected. This method is inexpensive but often will introduce some form of sampling bias and make it difficult to precisely calculate confidence intervals.
Common Non-Probability Sampling Methods
- Convenience sampling - Collecting samples in a way that is convenient to the researcher and might involve respondents that are located around an accessible location or Internet service.
- Quota sampling - Quotas for the target population are defined. Samples are selected from subgroups with similar characteristics, allowing for the chosen sample to meet demographic quotas.
- Snowball sampling - Participants are found with rare characteristics and are asked to find other similar participants from their own communities.
Survey Weights
Even if survey samples have been designed properly there will always be bias and error in the data. Weights are used to mitigate this by adjusting how much influence each individual has in the survey estimates.
Methods of Weighting Survey Data
Raking, matching and propensity weighting are different ways of adjusting the weight of demographic groups in survey data. It is also common to find them used in combination.
Raking ...
Consists of choosing a set of demographic variables like gender, age or education. Iteratively the weights of each individual are adjusted so the distribution of these variables amongst the sample population matches the distribution for the whole target population.
Matching ...
Is used to adjust non-probability samples. It starts with a sample representative of the target population, which then acts as a template for real survey data to be collected. This can be constructed from synthetic data or from a high-quality data source. Then, each individual from this sample is paired with the most similar individual from the collected data. When all matches have been found, unmatched individuals are discarded from the collected data.
Propensity weighting ...
Can be either used for probabilistic and non-probabilistic methods. Each individual from the target population has a certain probability of being selected. Propensity weighting assigns the inverse of this probability to each sample. In probabilistic methods this probability is known in advance. On the other side, for non-probabilistic methods, probability is estimated through statistical models.
There's SPSS. There's SAS and Then There's Graphext
Software like SPSS or SAS includes predefined functions to calculate survey estimates using predefined weights. But they lack visualisation capabilities and make it difficult to analyze variable combinations. That's where Graphext comes into play.
As opposed to SPSS or SAS, Graphext counts rows when calculating ratios and percentages for combinations of variables. This flexibility makes it easy to work with datasets of many shapes and sizes but doesn't consider the importance of survey weights.
Our team needed a method of transforming survey data so that the demographic sample with the smallest weight was represented at least by one row. Then we could scale the rest of the samples accordingly.
1. First, we obtain the scaling factor that converts the smallest weight into one.
2. Then, we scale the rest of the weights using this factor.
3. Next, each demographic sample in the original dataset would be represented by n rows in the transformed dataset. We round it to get an integer value - which introduces a negligible error.
4. As a final step, we duplicate the rows of the original dataset according to the calculated n rows for each demographic sample.
All this can be summarised in a few lines of Python code ...
n_samples_min = 1 # Here we set the nº of samples that represent the sample with the min weight in the transformed data
factor = n_samples_min / min(df[weight]) # Obtain the factor
df["n_rows"] = df[weight] * factor # Obtain the new number of rows for each sample
df["n_rows"] = round(df["n_rows"]) # Round the new number of rows, since we can only have integer rows
df_transformed = df.loc[df.index.repeat(df["n_rows"])].reset_index(drop=True) # Replicate rows as the column n_rows indicated into a new dataframe
A Case Study: Dating & Relationships in the American Trends Panel
This survey follows the standard methodology to conduct surveys implemented by the Pew Research Center. If you want to read more about survey theory - you could do a lot worse than reading about their methods here!
Sampling Method: Random Sampling using the U.S. Postal Service’s residential address file.
Weighting Method: Raking
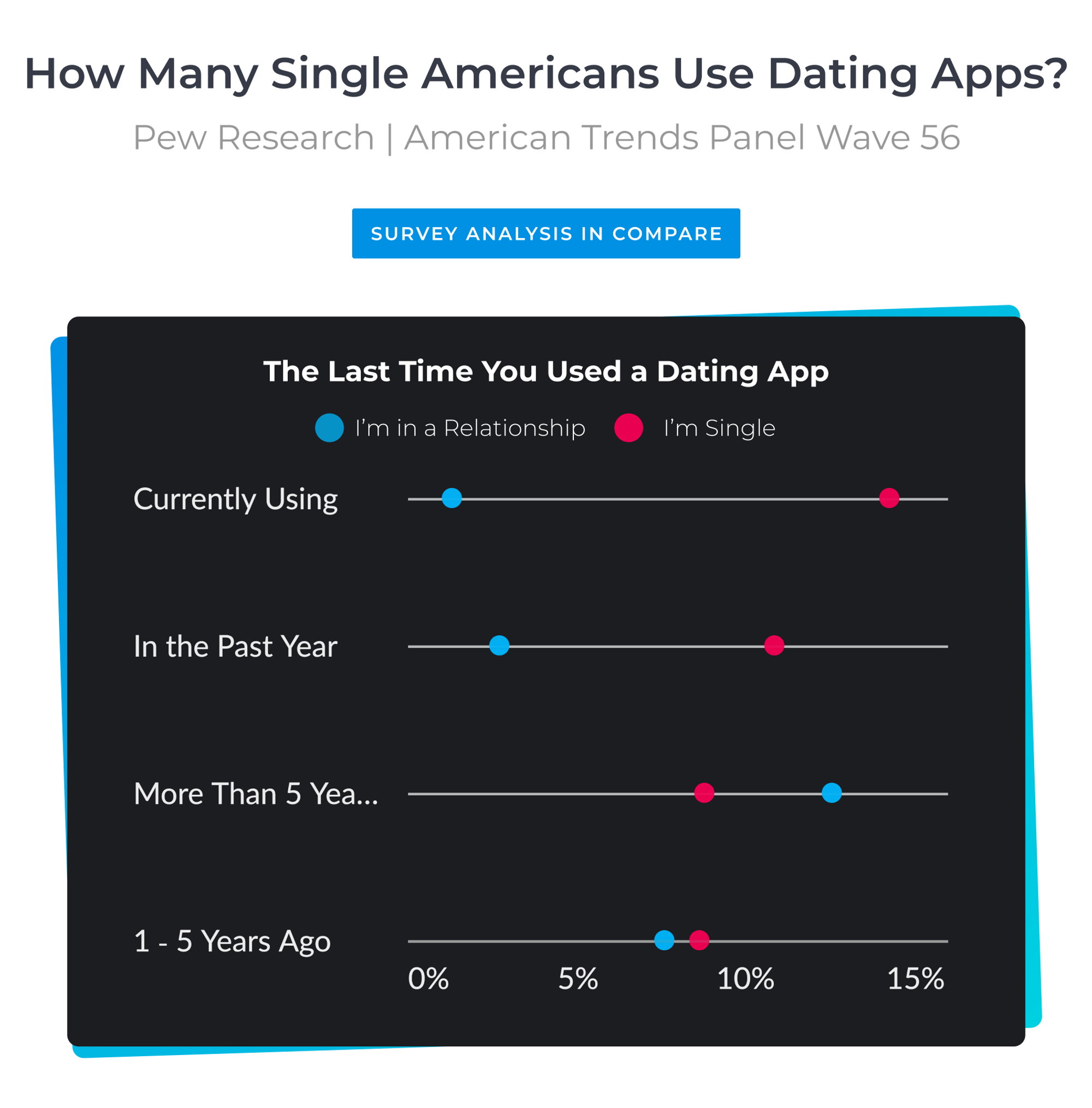
How Many Single Americans Use Dating Apps?
According to the survey estimates, around a quarter of single Americans are currently using dating apps or have used in the past year dating apps. That's 1 out of 4 singles. Given the fact that Tinder was only founded in 2012, this is a pretty sizable statistic reflecting how our attitudes towards dating apps have changed dramatically.
More or less 4% of people in a relationship are currently using or have used dating apps in the past year. It is worth highlighting that - no matter how well a survey is designed - some questions will always introduce bias. It's not difficult to imagine that some people lied in response to this question. We can probably assume therefore that this rate is even higher!
.png)
Is It Okay to Have Sex on a First Date?
In modern society, dating etiquette is complex and varied - especially so when it comes to sex. But the value of surveys like this one is in offering a glimpse at societies attitudes.
Almost 40% of men think it's always or sometimes ok to have sex on the first day against just 20% of women. Half of women, responding to this survey, feel that this is never acceptable.
.png)
It's worth pausing here to consider the impact of weights on this survey question. If the proportions of males vs female respondents were unbalanced in the original dataset, the data would present unrepresentative results.
But after considering weights with an upsampling technique, we are counting each individual with the importance she or he represents for the target population. The beauty of a well-designed survey is a fairer representation of what society thinks and feels.
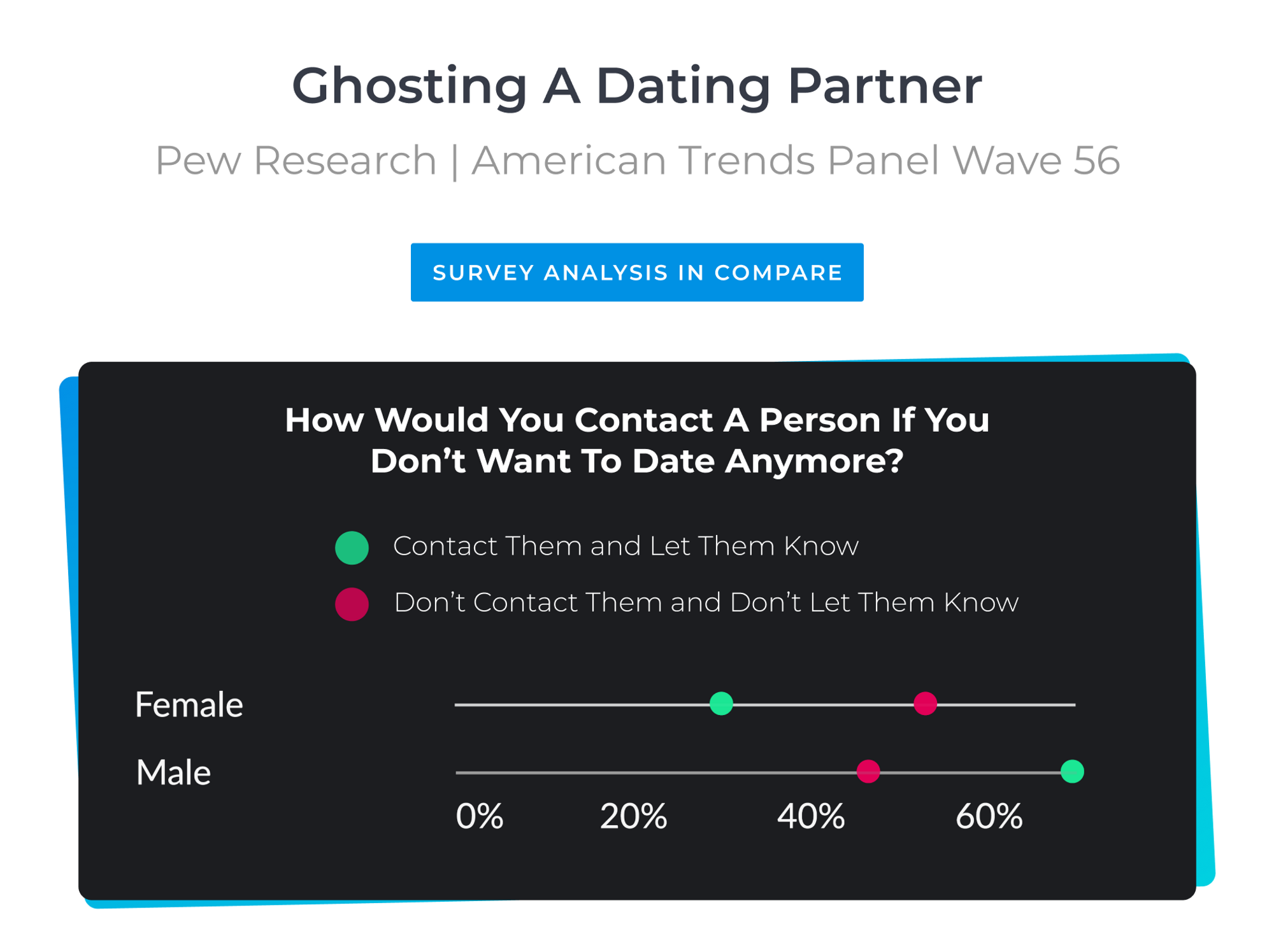
Who is More Guilty of 'Ghosting': Men or Women?
The culture behind dating apps has catalyzed the rise of some interesting new terms to define certain romantic - or unromantic - behaviours. "Ghosting" is a pretty nasty technique of not replying to someone in order to get them to leave you alone. Sorry if this is news to you but if you've been 'ghosted' - time to give up on the hope of hearing from this person ever again.
The survey conducted by Pew Research suggests that the majority of men (70%) do contact their date partners to let them know they don't want to have another date. Only 30% of women do the same.
.png)
You can find another interesting analysis performed by Pew Research Center using the same survey in the following links:
Key Points to Remember:
- The quality of a survey depends on the quality of the design and the sampling method. Probability sampling typically provides better results.
- Weights assign a certain relevance to each of the participants based on their representativeness with respect to the target population. One of the most popular weighting methods is Raking.
- At Graphext we use upsampling as a workaround for survey datasets - using weights without aggregating data - something which provides greater flexibility.
- When we are looking for general patterns and we don't care about high precision, it's okay to neglect weighting as long as we're working with a well-designed survey.
